Added (ab)Normals

I had a go at adding normals to all the vertices on the planet and it had a pretty dramatic effect. I started off with an algorithm from … here … site seems to be down at the moment though. Anyways, I converted it to work with triangle strips and got some pretty nice results:

I threw in another planet in the background to look like a moon, textures are still non-existent.

There are some problems with this technique though, namely that the vertices at the edges (and especially the corners) of patches calculate their normal from a smaller number of connections – so there’s always seams between patches, and exaggerated peaks at corners… looks a bit like the labels are coming off…

I *think* the solution is to either share the edges between patches (but that might force me to do SetData on 4 neighbouring patches – very slow), or for each patch to generate more data than it will show, e.g. a 1-cell skirt around the existing patch.

There’s also some weird effect going on around ridges, maybe because the diagonals are longer so should be weighted differently? I’m hoping it’ll go away when I use a normal map… after I figure out how to generate it first! :)

Other than that I put normals on the trees (much easier) and implemented a recycling scheme so patches that weren’t used wouldn’t keep a hold on memory. One result of all the above work is that there are cracks in the patches again so I’ll have to revisit my LOD decision stuff… one step forward, two steps back, then get hit by a bus.

L-System Trees

I continued working with the Algorithmic Beauty of Plants book and implemented parametric and context-sensitivity from chapter 1, made the trees from 3D tubes (instead of lines) and tried some of the examples from chapter 2 Modeling of trees. I had some success but couldn’t reproduce some of the models, mainly the section with tri-branching trees.

Here’s my results of the rules on page 56 varied with the parameters on page 57:

And here’s what the original ones from the book look like:

They look pretty similar, apart from (b). Note that in (b) the height of my version is the same as the other trees, but in the book it is much shorter. This is odd because the table on page 57 modifies the branch contraction rate (r₂) only, not the trunk contraction rate (r₂) which is always 0.9 so they should all be the same height.

In fact, it’s not clear what the height should be to get the above images as the axiom at the start sets the length to 1 and the width to 10, and if the length:width ratio really were 1:10, the result would be a lot more squat, like this:

And it’s still pretty squat at 10:10:

I found a ratio of 100:10 worked best to yield results similar to the book.

The experiments on page 59 looked pretty much identical to the book (again using a ratio of 100:10 so an initial axiom of A(100,10) instead of A(1,10)), here’s mine:

And here’s the books:

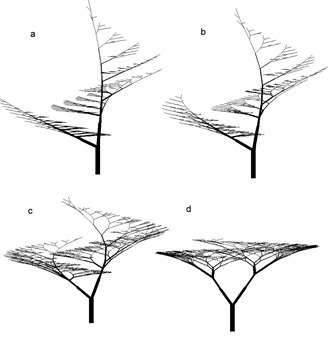
I had the least luck with reproducing the examples under Ternary branching. In the book (a) is shown as:

… which has a degree of irregularity… I don’t know where the model can get this as there is no stochasticity specified and the tropism applied is straight down (like the force of gravity), so why would the branch on the right bow down more than any other branch? My results show a much more regular model:

The closest of the ternary branching section I got was (b), although I had to fiddle with a few parameters (setting the width increase rate to 1.432 instead of the 1.732 given). Here’s the version in the book:

And here’s my result:

(c) and (d) were real headaches… I can’t get these to look anything like the ones in the book… I’m pretty sure something’s missing ar the parameters specified are wrong, especially the elongation rate (l_r) for (c); on page 61 it’s defined as 1.790 and all the others are 1.1 or less. Plugging this into my L-System/turtle interpreter results in a very tall tree (looking up at it in the first image and looking head on but zoomed out enough to see whole tree in the second):

I’m pretty sure my coding is right on this one, if you take the start piece from the axiom which is defined as F(200) and apply p2 (F(l) –> F(l*l_r) 8 times with l_r set to 1.790, this is the same as 200*(1.790⁸) which is about 21079. For the other trees, l_r is 1.109 and the base trunk height after 8 iterations of p2 would be 200*(1.109⁸) which is about 457. However the image in the book shows the tree as the same height and roughly the same proportion to its width as the other examples:

If I muck about with the parameters a bit I can get something that looks a bit more like it:

… but it’s not quite as nice. (d) is the same story really, can’t reproduce it from the parameters given… :(

I’m *pretty* sure I’m right but this book has been out since 1990 and there’s nothing specified in the errata. I tried to find these models in the virtual lab available from algorithmicbotany.org but no luck. So I might fire off an email and see if any one associated with the book can help me out…

Other than that I implemented horizon culling on the planet with a lot of help from an article at crappy coding, redid some of my basic rotation stuff (I had everything mirrored through the z axis), and tried to streamline how new patches are formed on the planet (it didn’t work!). I’m not sure what to do next, had a look at some demoscene programs and am now utterly depressed at how little I’ve done! I might try generating normal maps from the heightmap of a planet patch for lighting, maybe do atmospheric scattering, texturing of the planet and/or trees, adding leaves maybe? Hiring someone else to do this for me?? :)