L-Systems

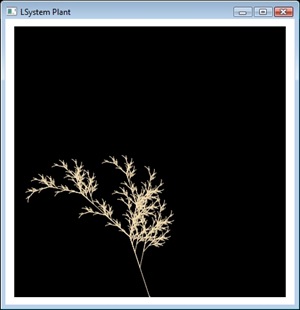
I spent some spare time today doing a first draft at an L-System.  I was always intrigued by how nature is apparently governed by mathematics like the Fibonacci sequence.  L-Systems are basically grammars used commonly to model growth as it occurs in nature and to develop self-similar fractals.  A stochastic L-System (an L-System where each possible change has a certain probability of being selected) is what was used in this procedural cities paper for SIGGRAPH 2001.  There are some other methods, but I don't think they are as realistic as what Mueller and Pascal had done.  The L-System (with some add-on rules) is used to draw out the streets and also to generate buildings with different LODs.  I'm not sure where to go from my basic random-blocks-on-a-plane so I decided to look into L-Systems to try and generate a realistic city.  But first things first, here's a fractal plant (L-Systems in WPF):

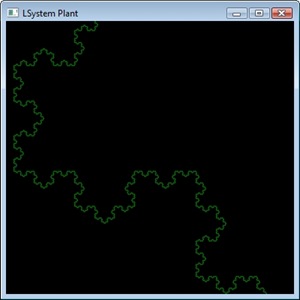
I coded a basic L-System and turtle graphics (something that draws whatever the L-System generates by following it like a path) and got the grammar for the plant on the wiki page.  It looks very like something you'd find in nature, but it all follows a strict grammar with only 2 rules and if you look for it, you can see the self-similar patterns.  It does take a while to execute however, especially at high iterations.  This site has a few of the common L-System grammars in a java app so you can play about with different grammars/iterations etc. and here's a gallery of other simple fractal forms.  Here's one more from my little app before I hit the hay - an arty close-up of part of a Koch snowflake:

I'll be honest, it's not arty, what it is is it's too fecking late to be messing about with WPF is what it is so screw you! Goodnight.

Sharing is a bad thing

I took a bit of time out to do some performance testing, partly avoiding procedural cities as I haven't a clue how to go forward but mainly to see what could cause my planet to be so slow when rendering a pretty low amount of polys.  I created a new project and ran some tests to get a benchmark, here are results for one patch getting larger as time goes on:

 

Sharing the one vertex buffer is pretty much worse than having no vertex buffer at all!  I tried to see if 50 objects each with their own buffers vs. each sharing the one buffer would make any difference, but nope:

 

Weirdly enough though, 75% of all pie-charts look like pac-man:

Creating and deleting buffers on the fly for the planet just won't work as I found with earlier experiments with quadtrees.  Although I did find out that the garbage collector can't clean up buffers because behind the scenes a load of events are hooked up and these all have references to the buffer.  Setting Device.IsUsingEventHandlers to false can turn this off.

Sharing isn't efficient either.  A bunch of buffers will have to be created on startup to be exclusively used by each patch.  Working out how many and what size will be another performance analysis job... is it simple enough that I can keep procrastinating procedural cities? ... probably not.

Welcome to Randomville

I had a quick bash at doing a procedural city with some very basic ideas I had - it's really simple but already looks city-like.  Check it out.

You can probably tell from looking at the images but all I'm doing is creating a grid of Mesh.Box(es) with random heights - biasing the height of boxes in the centre to be higher than the boxes on the outskirts.  This image might show it a little more clearly.

In the next image I randomly eliminated some of the boxes (biasing the elimination more towards the edge than towards the centre).  I think it looks a little more realistic.

Flying around the city really gives a better city-feeling than looking at a bunch of boxes.  I tried to record a video but I couldn't get a smooth flyover using my touchpad and my *ahem* skills.  It doesn't look too bad but I won't post it as I'd be worried if someone saw my flying skills they'd think I was planning another 9/11.